[1]

Při dlouhodobém styku materiálu ve vlhké atmosféře dochází k transportu vodní páry materiálem (navlhání). Molekuly vody postupují při tomto procesu od povrchu materiálu, který je ve styku s vlhkou atmosférou, směrem dovnitř materiálu. V případě organických materiálů dochází k pronikání vlhkosti do materiálu difuzí vodní páry. Tento druh transportu vodní páry je označován jako aktivovaná difuze. Procesem aktivované difuze probíhá navlhání většiny izolantů z makromolekulárních organických látek. Podstata všech názorů na aktivovanou difuzi v polymerech spočívá v tom, že difundující částice jednak vibruje, jednak se pohybuje postupně do stále nových rovnovážných pozic. pokud částice získává dostatečné množství kinetické energie (aktivační energie). Ve většině polymerů je této aktivační energie zapotřebí pro tzv. „tvorbu děr“ v polymeru, tj. k separaci částí makromolekul polymeru.

Mechanizmus difuze vysokomolekulárními organickými látkami lze rozdělit do tří základních strukturálních typů:

Difuze I. typu předpokládá, že v látce neexistují žádné prostory trvalého charakteru. Látka se vyznačuje velkou pohyblivostí jednotlivých článků makromolekul. Molekula vody koná v látce vibrační pohyb kolem určité polohy, dokud se pohybem článků sousedních řetězců nevytvoří mezery, do níž může molekula vody difundovat. Opětným přiblížením článků makromolekul se difundující molekula zastaví a vibruje opět kolem určité polohy. Tímto způsobem projde molekula vody řadou mezer. Pravděpodobnost tvorby mezer je malá a difuze molekul vody je tedy pomalá.

Difuze II. typu vychází z představy, že jednotlivé články makromolekul mají omezenou pohyblivost a kmitají kolem určitých poloh s omezeným stupněm volnosti. V takovýchto látkách existují vnitřní prostory trvalého charakteru (preexistující). Na vnitřním povrchu existují adsorpční místa (hydrofilní radikály), na které se vážou molekuly vody. Molekula, která je adsorbovaná v adsorpčním místě není v klidu, ale kmitá kolem určité rovnovážné polohy tak dlouho, dokud nedosáhne energie pro desorpci, při které může přejít nesousední adsorpční místo. Aktivační energie E_a se v tomto případě spotřebuje na vypaření adsorbované molekuly.

Difuze III. typu počítá s výskytem obou předchozí typy difuze. Objevuje se u většiny polymerních látek.

K difuzi dochází vždy, když gradient koncentrace částic v daném směruje různý od nuly. Obecně je difuze popsána Fickovými zákony¹⁾, které se uvádějí v diferenciálním tvaru (rov 1, rov 2) :

I.

II.

Obr.1 Transport vodní páry deskou (I. Fickův zákon)

Množství difundujících molekul dm, které projdou za jednotku času jednotkovou plochou, kolmou ke směru difuze se nazývá hustota difuzního toku J, c je koncentrace vodní páry a D je difuzní koeficient. I. Fickův zákon platí pouze pro ustálený stav (obr.1).

Obr.2 Transport vodní páry deskou (II. Fickův zákon)

Chceme-li postihnout časovou změnu koncentrace, musíme použít II. Fickův zákon, který charakterizuje neustálený stav. Hustota difuzního toku je přímo úměrná gradientu koncentrace dc/dx, kde c je koncentrace částic v místě x (obr.2). Záporné znaménko v tomto vztahu vyjadřuje, že difuze směřuje z míst s vyšší koncentrací do míst s nižší koncentrací. Difuzní koeficient závisí na koncentraci difundující složky, na polohových souřadnicích a na čase.

Budeme-li uvažovat, že difuzní koeficient je konstantní, je možno získat obecné řešení difuzních rovnic pro nejrůznější počáteční a okrajové podmínky. Pro studium navlhání izolantů je nejběžnější případ difuze do materiálu ve tvaru rovinné desky. Rovinnou desku si představujeme jako prostor ohraničený dvěma rovnoběžnými plochami (x = 0 a x = d, šířka desky d). Množství vodní páry M, které projde deskou můžeme vyjádřit vztahem²⁾ (rov 3)

Při úvahách o pronikání vlhkosti do materiálu jsme operovali s difuzním koeficientem³⁾. Difuzní koeficient je veličina závislá na teplotě. Tuto závislost lze vyjádřit rovnicí Arrheniova typu (rov 4) :

Kde E_p je aktivační energie pro difuzi a D₀ je hodnota difuzního koeficientu při absolutní nule. Difuzní koeficient je „neměřitelná“ veličina. Odvozené vztahy pro rozložení koncentrace vlhkosti v rovinné desce umožňují stanovit koeficient propustnosti materiálu, který může simulovat difuzní koeficient.

Obr.3 Měření propustnosti

Koeficient propustnosti se zjišťuje experimentálně. Uspořádání experimentu pro měření propustnosti je takové, že vzorek (membrána), jejíž propustnost zjišťujeme, odděluje dva prostory. Jeden z nich obsahuje penetrát (vodní páru) o konstantním tlaku p₁, ve druhém je penetrát udržován na tlaku p₂ < p₁, přičemž na začátku pokusu neobsahuje membrána žádnou sorbovanou vodu. V ustáleném stavu lze s ohledem na předcházející výraz odvodit vztah (rov 5) :

kde P je koeficient propustnosti, který udává množství plynu, které projde za normálních podmínek za 1 s jednotkovou plochou S o jednotkové tloušťce d membrány při rozdílu tlaku p₂ - p₁.

Z I. Fickova zákona vyplývá souvislost mezi difuzním koeficientem a koeficientem propustnost (rov 6) :

Poměr c/p je Henryho zákoně konstanta rozpustnosti s takže pro koeficient propustnosti platí vztah (rov 7) :

Základním typem transportu vody v makromolekulárních organických látkách při jejich navlhání v prostřední vodní páry je difuze. U některých technických, zejména nehomogenních izolantů, jsou však pozorovány odchylky od tohoto degradačního procesu. Ve většině případů jsou způsobeny tím, že difuze jako základní děj je provázena ději dalšími. V kapilárně porézních látkách se mohou uplatnit následující typy transportu vody:

Představme si, že máme dva volné prostory, které navzájem spojuje válcová kapilára. Prostory jsou vyplněny směsmi vodní páry se vzduchem, jež mají stejnou teplotu a tlak. Jejich složení (parciální tlaky plynů v obou směsích) se však liší. Vyrovnání těchto rozdílů se děje difuzí, jež probíhá beze změny teploty i tlaku. Molekuly vodní páry budou difundovat vzduchem v kapiláře zleva doprava, molekuly vzduchu zprava doleva.

Obr.4 Volná difuze v trubici

Pomocí kinetické teorie plynu lze vyrovnání rozdílů v koncentracích obou plynů vysvětlit tepelným pohybem a srážkami molekul. Tento proces neprobíhá u obou plynů stejně rychle. Molekuly lehčího plynu proniknou za stejnou dobu dál než molekuly plynu těžšího. Tím by se ale porušila tlaková rovnováha směsi. Aby k tomu nedocházelo, musí tepelný (chaotický) pohyb překrývat proudění. Vysvětlený mechanizmus proudění je podstatou volné difuze v porézní látce. Aby se jednalo o volnou difuzi, musí mít póry větší poloměr než je střední volná dráha molekul difundujícího plynu. A to proto, aby bylo možné zanedbat srážky molekul plynu se stěnami pórů.

Obr.5 Povrchová difuze

U porézních látek je možná i tzv. povrchová difuze. K povrchové difuzi dochází proto, že adsorbované molekuly mají na povrchu určitou pohyblivost. Zachycují se sice na určitých místech povrchu s vyvinutými adsorpčními silami (adsorpční místa), avšak i mezi těmito místy je možný přechod.

Mějme opět válcovou trubici, jež spojuje dva prostory o různém tlaku plynu, avšak jejíž rozměr je velmi malý v porovnání se střední volnou dráhou molekul plynu. Molekuly plynu procházející

Obr.6 Molekulární proudění

trubicí z místa vyššího tlaku na místo nižšího tlaku, se v tomto případě řídí zcela jiným zákonem než je zákon laminárního toku plynu. Tento zákon se nazývá Knudsenovo molekulární proudění. Je-li střední volná dráha molekuly větší než rozměr kapiláry, nelze již považovat plyn za kontinuím a při výkladu mechanických a tepelných vlastností plynu musíme vycházet z kinetických představ. Teorie se velmi zjednoduší, je-li střední volná dráha značně větší než rozměr kapiláry. V tom případě je počet vzájemných srážek molekul v prostoru kapiláry nepatrný a zanedbatelný oproti počtu srážek molekul se stěnami kapiláry. Molekula se pohybuje trubicí stálou rychlostí po přímé dráze tak dlouho, až narazí na stěnu. Kdyby byla stěna absolutně hladká a neadsorbující, odrážely by se od ní všechny molekuly pružně. Ve skutečnosti se část molekul dopadajících na stěnu pružně odrazí, zatímco zbytek je stěnou adsorbován a po určitém prodlení na povrchu stěny vysílán ve všech směrech stejnoměrně, nezávisle na tom,jaké byly rychlosti a směry molekul dopadajících. Tento jev se nazývá difuzní reflexe.

Obr.7 Zkondenzované množství vodní páry na povrchu ochlazeném na teplotu rosného bodu

Dojde-li k prudké změně teploty prostředí, vyrovnávání teploty mezi okolím a povrchem materiálu se odehrává v mezní vrstvě nad povrchem (rosný bod). Vzduch se v této vrstvě nasytí vodní párou a protože relativní vlhkost nemůže překročit 100 %, zbytek vody se vysráží na povrchu ve formě zkondenzované vody. O množství

Obr.8 Kondenzace vodní páry na povrchu- rosný bod

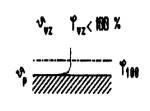
takto vzniklé vody na povrchu si lze učinit představu z obr.7. K obdobnému jevu dochází i ve vzduchu na kondenzačních jádrech prachu, nečistotách. Takto zkondenzovaná vodní pára může na povrchu a vytvářet vrstvy vody v kapalné fázi. Protože množství vody vzniklé těmito mechanizmy na povrchu materiálu je mnohonásobně větší než popsanými sorpčními jevy, je i vlhkostní znehodnocení materiálu výraznější. Zejména tehdy, je-li k tomu ještě povrch znečištěn rozpustnými látkami.